Solar Tracking With A Box-Style Cooker
by James W. Thomasson, PhDArlington Virginia USA
E-mail: Jim_Thomasson@yahoo.com
How do you keep your solar cooker aimed at the sun? As a practical question, if you can get your alignment within 30 degrees of the sun then it is probably close enough. You just have to change the orientation of the box or reflectors every hour or so.
In comparison for a panel-style cooker, you don't have very many choices except to
move the cooker. A large
parabolic reflector
would have to be much more accurately aligned. And that will cost you some
money. Or you can make your solar oven 20 feet long and use
a trough reflector. Or you can go out every hour and move the cooker.
The box-style cooker has adjustable reflectors. Why can't we rotate the reflectors,
instead of moving the whole box? They don't weigh very much. You can mount
them on hinges.
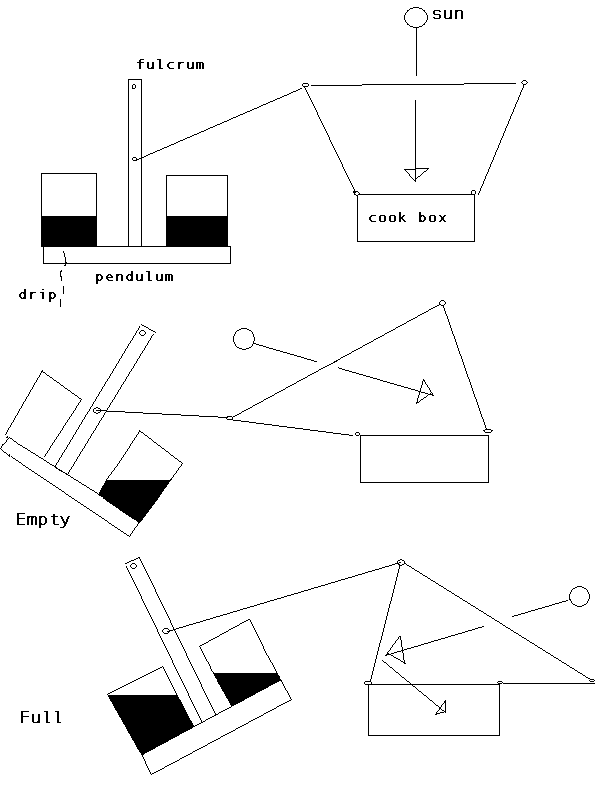
In this document, I show some sketches about how to build a pendulum mechanism
that pulls on a string that moves the reflectors on a cooking box.
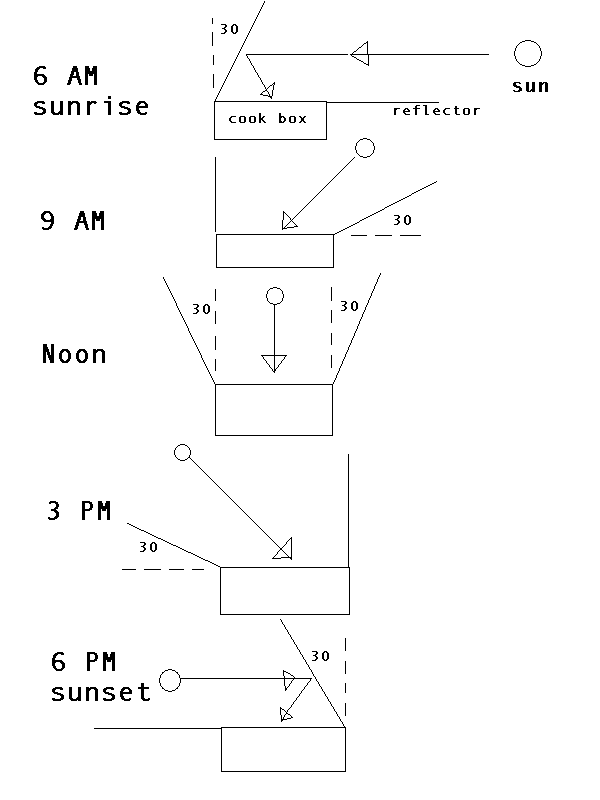
What are the angles of the reflectors? It took me awhile to remember enough
trigonometry and physics to figure it out. Plus a little help from
Dr. Math. After writing a computer program to compute the angles, I
discovered that it is a very simple formula. I assume that the reflector is the
same size as the window on the cooking box, and hinged at the edge of the
window. If the sun is directly overhead, then the reflectors lean out
about 30 degrees away from the box. The reflectors rotate 10 degrees
per hour. (The sun moves 15 degrees per hour.) At 9 AM (or 3 PM), the sunward
reflector is about 30 degrees above horizontal and the other reflector is
vertical. At sunrise (or sunset), the sunward reflector is horizontal (it doesn't reflect
any useful amount of sunlight) and the other reflector leans about 30 degrees
towards the sun, over the top of the cooking box.
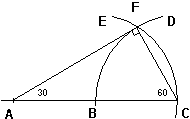
How big is a 30-degree angle? You can construct an equilateral triangle with
dividers and straightedge, then cut it in half. From this you get 2 triangles each
with a 30-degree angle. Another way to do it is shown in the following
illustration. With dividers and straightedge, construct line BC equal
to AB. Draw an arc D with radius equal to AB centered on point C. From point
B construct another arc E with the same radius, intersecting D at point F. With
straightedge, draw lines CF and AF. Triangle ACF will have a 30-degree angle,
a 60-degree angle, and a right angle.
We need a mechanism to move the reflectors slowly, tracking the sun. I estimate
that a reflector weighs about a pound since it is made of cardboard and aluminum
foil. If we put a full 5-gallon bucket of water on one side of a pendulum
and a half-full bucket on the other side, then I think
that would give enough force to lift the reflectors by pulling on a string or
something. The pendulum is about 3 feet long, suspended on a fulcrum
about 4 feet above the ground. The pendulum supports a rigid platform
about 4 feet long. Fasten the buckets to opposite ends of the platform.
To drain a 5-gallon bucket in 8 hours, you need about 8 drops per second. Let
the water drain into your garden! (This estimate is based on
46,080 drops per U.S. Gallon. Measure for Measure,
Richard A. Young and Thomas J. Glover (1996,
Blue Willow, Inc.,
Littleton Colorado USA), pg. 289.)
How can we get a device that reliably drips 8 per second? It is not
a drip-drip-drip, but more of a dip-p-p-p-p-p-p-p. I wouldn't put a hole
in the bucket if I don't have to. Let's try siphoning the water out of the
bucket. Stuff some cloth in the end of the siphon hose so that it drips, instead
of flows. This is adjustable, by stuffing more or less cloth into the hose.
If you counterbalanced the reflectors, then you might be able to do it with
1-gallon buckets instead of 5. It might be worth the extra effort to
counterbalance them. At least the pendulum mechanism would not weigh
100 lbs. I think that you need the weight of 5 gallons of water,
about 40 lbs, to lift reflectors that don't have counterbalances. You
also don't want them to blow with the wind.
The distance between the tips of the reflectors is a few percent smaller than
twice the size of the reflector. You can connect them together with a stick
or piece of bamboo or a stiff wire or something.
Find a location on the pendulum mechanism that moves in 6 hours through a distance
that is equal to the size of the reflector,
or 1.732 times the size of the reflector in 12 hours. Connect
that location on the pendulum to one of the reflectors. As the water
drains out of the 5-gallon bucket, it pulls the reflectors on the cooker.
I have not tested any of this to find out whether or not it works. Maybe I
can find time to try it later this year.